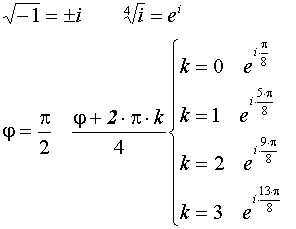19.Формула Тейлора. Остаточный член в форме Пеано и в форме Лагранжа.
Высшая математика — просто и доступно! Математические формулы, таблицы и другие материалы. Книги по математике. Высшая математика для чайников, или с чего начать?



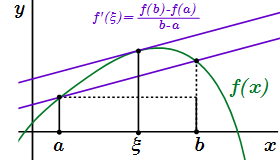
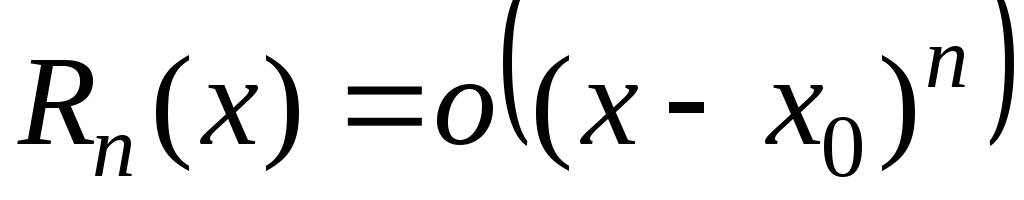
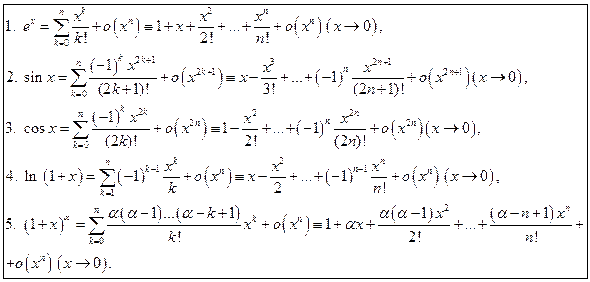

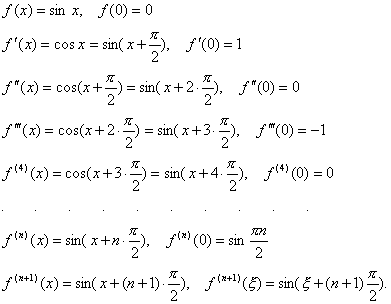

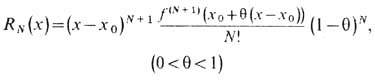

Применим метод математической индукции. Из равенств 2 и 3 получаем:. Боярчук "Функции комплексного переменного: теория и практика" Справочное пособие по высшей математике.
- На страницу Пред.
- Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, так как функция по-разному опрделена в нуле и вне нуля.
- Конев В. Дифференцирование функций.




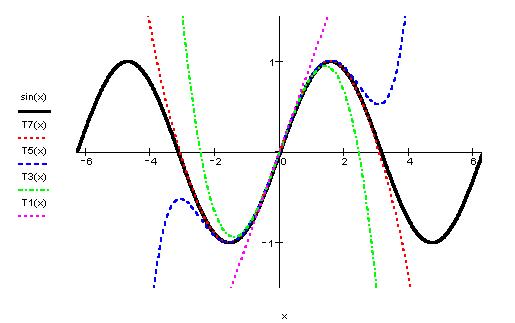
Конев В. Дифференцирование функций. Разделы курса Примеры Калькулятор. Пределы Неопределенные интегралы Определенные интегралы Несобственные интегралы.