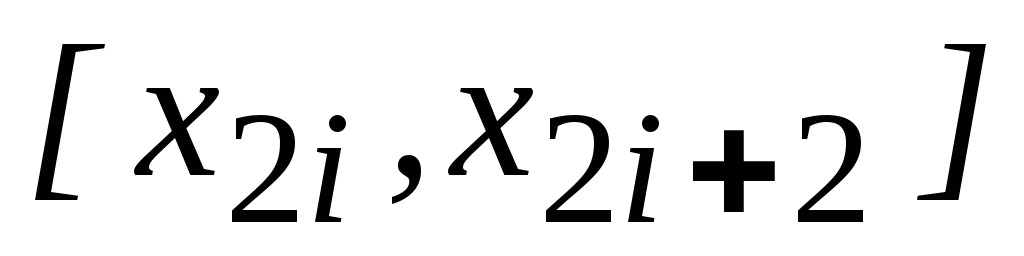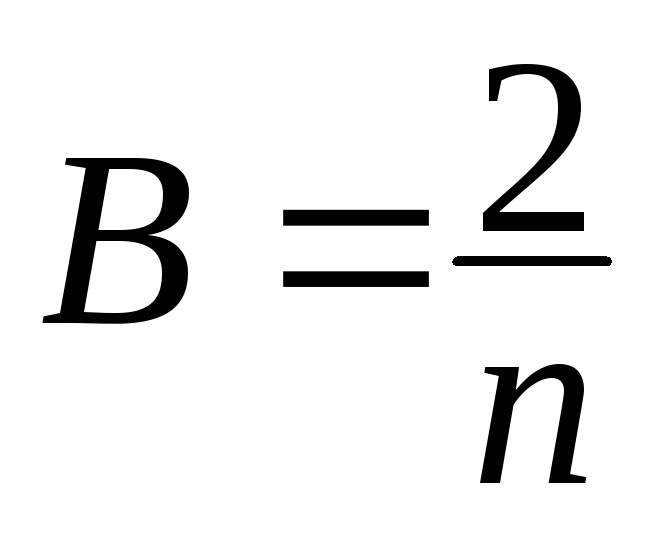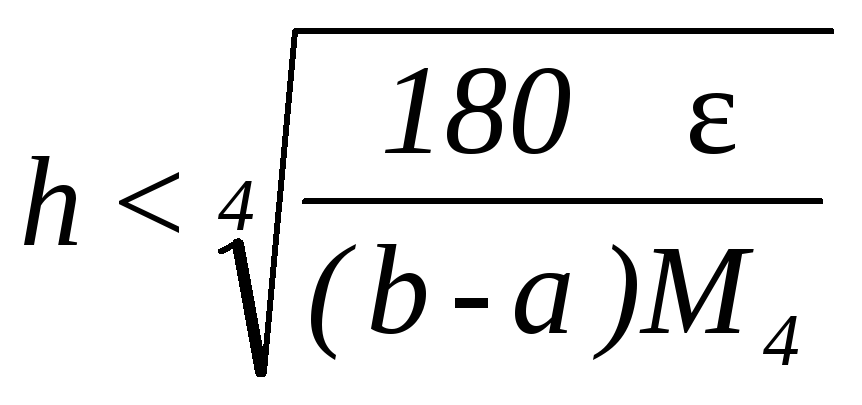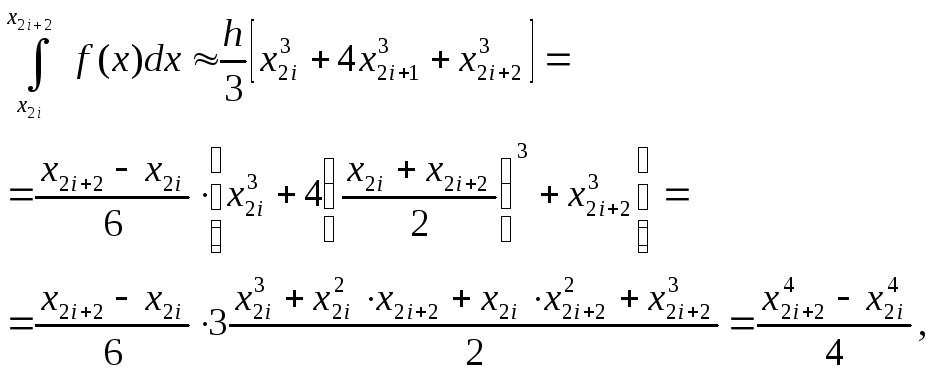§2.1 Квадратурные формулы интерполяционного типа.
Высшая математика — просто и доступно! Математические формулы, таблицы и другие материалы. Книги по математике. Высшая математика для чайников, или с чего начать? Повторяем школьный курс.

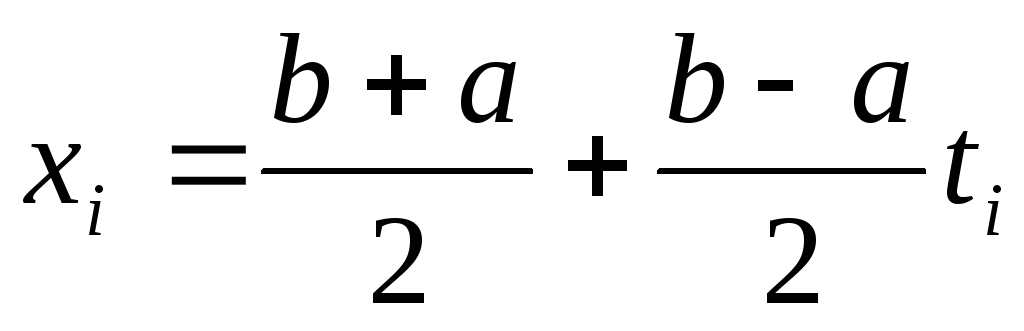






Формула Симпсона. Предположим, что. Заменим функцию f x на каждом отрезке длиной 2 h интерполяционным полиномом Лагранжа второй степени и положим. Возьмем интеграл в правой части 6.
- §2.2 Организация программ.
- Применяя формулу Симпсона к каждому удвоенному промежутку длины 2h , будем иметь. Введя обозначения , формулу можно записать в более простом виде:.
- Квадрат у рные ф о рмулы формулы, служащие для приближённого вычисления определённых интегралов по значениям подинтегральной функции в конечном числе точек. Наиболее распространённые К.
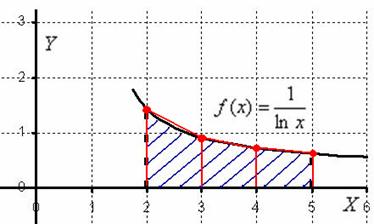
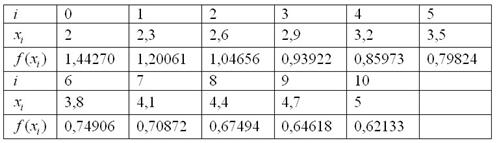
- При использовании численных методовопределенный интеграл 4. Веса и узлы определяются методом интегрирования, а также областью и не зависят от подынтегральной функции f х.
- §2.2 Организация программ.
- Формула Симпсона также Ньютона -Симпсона [1] относится к приёмам численного интегрирования.
- Если подынтегральная функция четырежды дифференцируема, то остаточный член квадратурной формулы Симпсона равен:.
- More Related Content. Методы численного интегрирования 1.
- Вычислительная математика
- На прошлой лекции были выведены формулы Ньютона-Котеса.